Gerak Parabola
Gerak Parabola juga dikenal sebagai Gerak Peluru. Dinamakan Gerak parabola karena lintasannya berbentuk parabola, bukan bergerak lurus. Contoh bentuk gerak ini dapat kita lihat pada gerakan bola saat dilempar, gerakan pada peluru meriam yang ditembakkan, gerakan pada benda yang dilemparkan dari pesawat dan gerakan pada seseorang yang melompat maju.
Agar kamu memahami materi ini dengan baik, kamu harus memahami terlebih dahulu materi berikut:
- Operasi Vektor
- Gerak Jatuh Bebas
- Gerak Lurus (GLB dan GLBB)
Untuk mempermudah pemahaman kamu, perhatikan gambar lintasan gerak parabola dan komponennya di bawah ini.

Jika kita memerhatikan gambar diatas, kita dapat menyimpulkan bahwa gerak parabola memiliki 3 titik kondisi,
Pada titik A, merupakan titik awal gerak benda. Benda memiliki kecepatan awal  .
.
Pada titik B, benda berada di akhir lintasannya.
Pada titik C, merupakan titik tertinggi benda. Benda berada pada ketinggian maksimal  , pada titik ini kecepatan vertikal benda besarnya 0 (nol) (
, pada titik ini kecepatan vertikal benda besarnya 0 (nol) (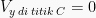 ).
).
Komponen Gerak pada Gerak Parabola
Gerak Parabola merupakan gabungan dari dua komponen gerak, yakni komponen gerak horizontal (sumbu x) dan komponen gerak vertikal (sumbu y).
Mari kita bahas kedua komponennya:
- Komponen gerak parabola sisi horizontal (pada sumbu X):
- Komponen gerak horizontal besarnya selalu tetap dalam setiap rentang waktu karena tidak terdapat percepatan maupun perlambatan pada sumbu x
, sehingga:
- Terdapat sudut (θ) antara kecepatan benda (V) dengan komponen gerak horizontal
dalam setiap rentang waktu, sehingga:
- Karena tidak terdapat percepatan maupun perlambatan pada sumbu X, maka untuk mencari jarak yang ditempuh benda (x) pada selang waktu (t) dapat kita hitung dengan rumus:
- Komponen gerak horizontal besarnya selalu tetap dalam setiap rentang waktu karena tidak terdapat percepatan maupun perlambatan pada sumbu x
- Komponen gerak parabola sisi vertikal (pada sumbu y):
- Komponen gerak vertikal besarnya selalu berubah dalam setiap rentang waktu karena benda dipengaruhi percepatan gravitasi (g) pada sumbu y. Jadi kamu harus pahami bahwa benda mengalami perlambatan akibat gravitasi
- Terdapat sudut [θ] antara kecepatan benda (V) dengan komponen gerak vertikal
, sehingga:
- Karena dipengaruhi percepatan gravitasi, maka komponen gerak vertikal
pada selang waktu (t) dapat kita cari dengan rumus:
- Kita dapat mencari ketinggian benda (y) pada selang waktu (t) dengan rumus:
- Komponen gerak vertikal besarnya selalu berubah dalam setiap rentang waktu karena benda dipengaruhi percepatan gravitasi (g) pada sumbu y. Jadi kamu harus pahami bahwa benda mengalami perlambatan akibat gravitasi
- Terdapat pula persamaan-persamaan untuk menentukan besaran gerak parabola lainnya:
- Apabila tidak diketahui komponen waktu, kita dapat langsung mencari jarak tempuh benda terjauh (
), yakni dari titik A hingga ke titik B, dengan menggabungkan kedua komponen gerak.
Komponen gerak horizontal:
Komponen gerak vertikal:
Dengan mensubstitusikan kedua persamaan diatas, kita mendapatkan persamaan: - Kita dapat pula langsung menghitung ketinggian benda maksimum
dengan persamaan:
- Selain itu, dengan dengan menggunakan teorema Pythagoras kita dapat mencari kecepatan benda jika kedua komponen lainnya diketahui.
- Jika diketahui kedua komponen kecepatan, kita juga dapat mengetahui besarnya sudut θ yang dibentuk, yaitu:
- Apabila tidak diketahui komponen waktu, kita dapat langsung mencari jarak tempuh benda terjauh (
Contoh Soal Gerak Parabola
Soal 1:
Seorang stuntman melaju mengendarai sepeda motor menuju ujung tebing setinggi 50 m. Berapa kecepatan yang harus dicapai motor tersebut saat melaju dari ujung tebing menuju landasan dibawahnya sejauh 90 m dari tebing? Abaikan gesekan udara.
Pembahasan:
Gambarkan terlebih dahulu lintasan gerak parabola objek tersebut. Perhatikan gambar dibawah ini:

[Sumber: Douglas C. Giancoli, 2005]
Kemudian kita identifikasi komponen-komponen yang diketahui,
Dengan rumus untuk mencari ketinggian benda, kita bisa mendapatkan waktu tempuh:
Dengan rumus untuk mencari jarak tempuh, kita bisa mendapatkan kecepatan motor:
Jadi, kecepatan yang harus dicapai harus sebesar 28,21 m/s atau sekitar 100 km/h (101,55 km/h).
SOAL 2
Sebuah bola ditendang membentuk sudut ( ) dengan kecepatan . Hitunglah (a) ketinggian maksimum bola, (b) waktu tempuh bola hingga bola mendarat di tanah (c) seberapa jauh bola mencapai tanah, (d) kecepatan bola di ketinggian maksimum, dan (e) percepatan saat ketinggian maksimum. Abaikan gesekan udara dan rotasi pada bola.
) dengan kecepatan . Hitunglah (a) ketinggian maksimum bola, (b) waktu tempuh bola hingga bola mendarat di tanah (c) seberapa jauh bola mencapai tanah, (d) kecepatan bola di ketinggian maksimum, dan (e) percepatan saat ketinggian maksimum. Abaikan gesekan udara dan rotasi pada bola.
Pembahasan:
Gambarkan terlebih dahulu lintasan gerak parabola objek tersebut. Perhatikan gambar dibawah ini.

[Sumber: Douglas C. Giancoli, 2005]
Kita cari kedua komponen kecepatannya:
(a) Dengan menggunakan rumus kecepatan komponen vertikal, kita mendapat selang waktu tempuh saat bola mencapai titik tertinggi.
Kemudian, kita pakai rumus untuk mencari ketinggian benda:
(b) dan (c):
Pertama, kita pakai rumus untuk mencari jarak tempuh maksimum:
Pertama, kita pakai rumus untuk mencari jarak tempuh maksimum:
Mau diskon 40% paket RuangGuru? WA: 0813 7693 4946
Kemudian, kita dapat mencari jarak tempuh bola maksimum:
(d) Di titik tertinggi, tidak terdapat komponen kecepatan vertikal. Jadi kecepatan bola saat di titik tertinggi adalah:
(e) Besarnya percepatan sama di setiap lintasan, yakni sebesar 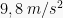 ke bawah.
ke bawah.

No comments:
Post a Comment